その1
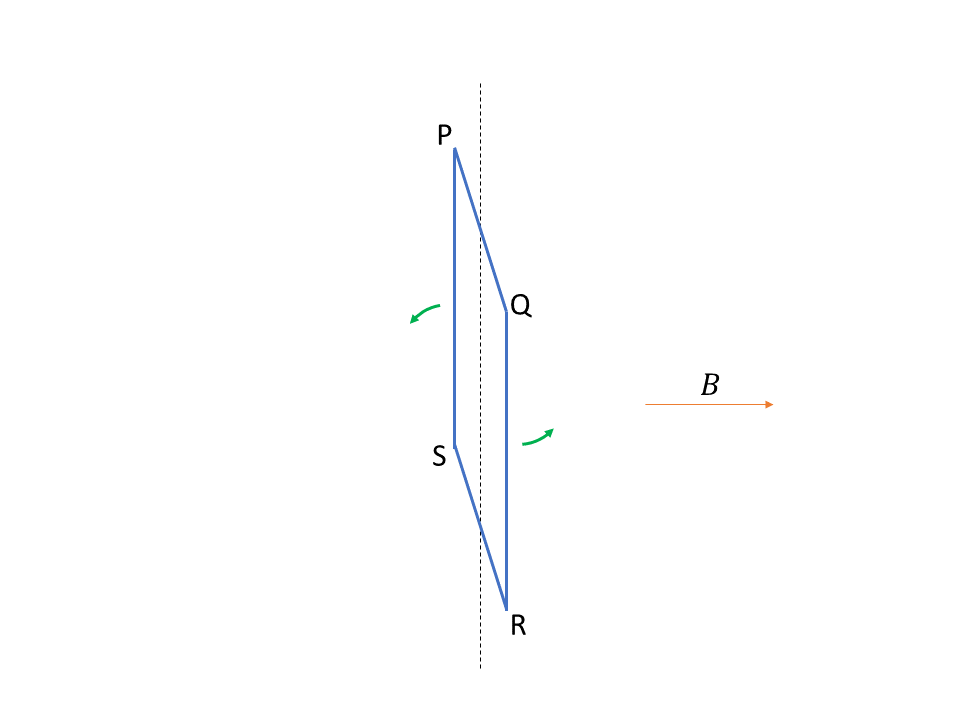
横 \(L_a\)、縦 \(L_b\) の長方形のコイルを考えます。このコイルを、磁束密度 \(B\) の一様な磁場の中に、縦の対称軸が磁場の向きと垂直になるように置きます。そして、縦の対称軸のまわりに一定の角速度 \(\Omega\) で回転させます。このとき、コイルに生じる起電力を考えます。
コイルの中心を原点にとります。そして回転軸を \(z\) 軸にとり、磁場の向きに \(x\) 軸をとります。コイルが \(yz\) 面上にきた時刻を \(t=0\) とします。\(t=0\) におけるコイルの頂点 P、Q、R、S の座標は \[ \mathrm{P}\left(0,\frac{L_a}2,\frac{L_b}2\right),\ \mathrm{Q}\left(0,-\frac{L_a}2,\frac{L_b}2\right),\ \mathrm{R}\left(0,-\frac{L_a}2,-\frac{L_b}2\right),\ \mathrm{S}\left(0,\frac{L_a}2,-\frac{L_b}2\right) \] となります。\(z\) 軸の正の向きから見ると次の図のようになります。
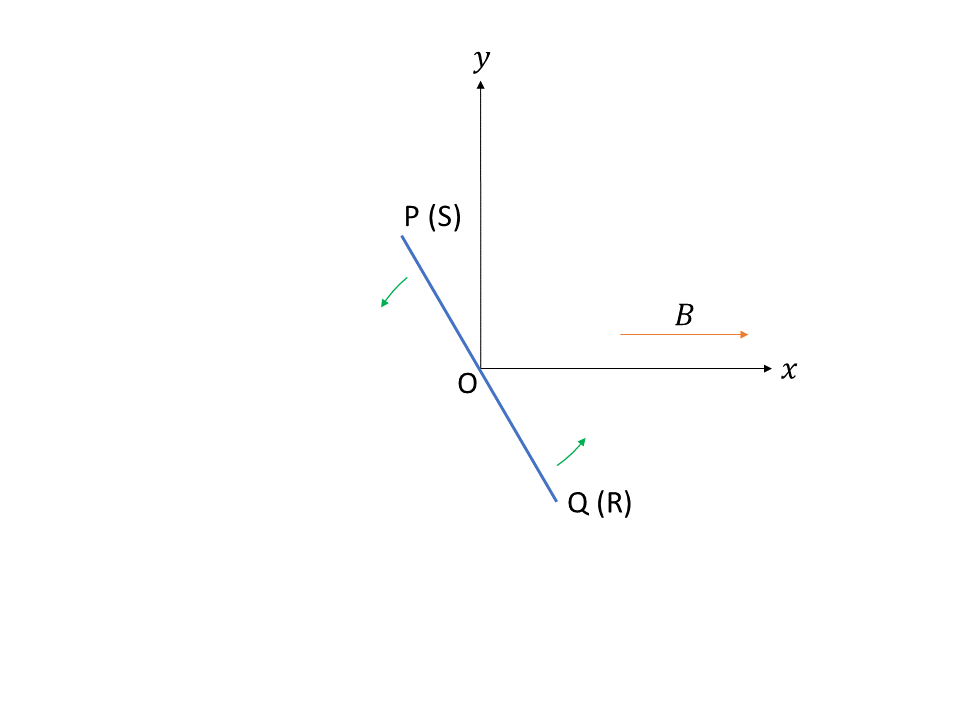
コイルに生じる起電力は、単位電荷あたりの力 \(\boldsymbol{v}\times\boldsymbol{B}\) をコイルにそって線積分したもの、すなわち \({\displaystyle\oint(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}}\) です。\(\boldsymbol{v}\times\boldsymbol{B}\) がコイルのどの部分でも \(z\) 軸に平行であることに注意すると \begin{eqnarray} \int_{\mathrm{P}\rightarrow\mathrm{Q}}(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}&=& 0\\ \int_{\mathrm{Q}\rightarrow\mathrm{R}}(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}&=& -\left(-\frac{L_a\Omega}2B\sin\Omega t\cdot L_b\right) =\frac{BS\Omega}2\sin\Omega t\\ \int_{\mathrm{R}\rightarrow\mathrm{S}}(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}&=& 0\\ \int_{\mathrm{S}\rightarrow\mathrm{P}}(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}&=& \frac{L_a\Omega}2B\sin\Omega t\cdot L_b =\frac{BS\Omega}2\sin\Omega t \end{eqnarray} となります。ただし \(S=L_aL_b\)(コイルの囲む面積)です。よって、コイルに生じる起電力は \[ \oint(\boldsymbol{v}\times\boldsymbol{B})\cdot d\boldsymbol{r}=BS\Omega\sin\Omega t \] となります。
その2
次に、\(z\) 軸のまわりに、角速度 \(\Omega\) で回転する座標系を考えます。この4次元座標系を \(K'\) 系と呼び、「その1」で考えた系を \(K\) 系と呼ぶことにします。\(K'\) 系から見ると、コイルは静止して見えます。\(K'\) 系は\(K\) 系と違って非慣性系なので、一般相対論的考察が必要です。
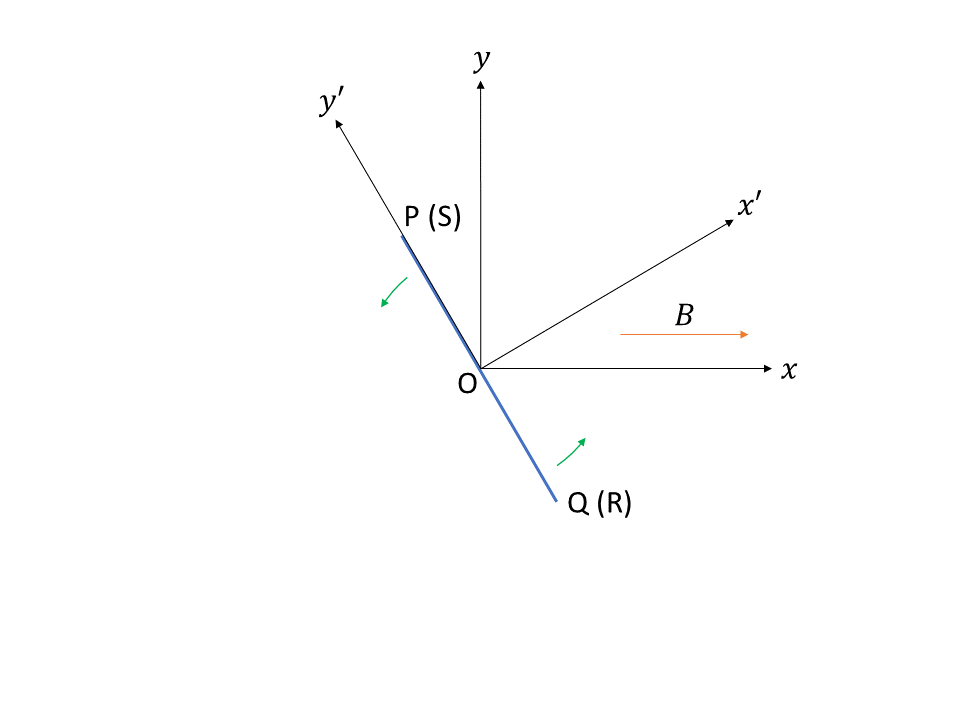
\(K\) 系の4次元座標を \(K'\) 系の4次元座標で表すと \begin{eqnarray} ct&=& ct'\\ x&=& (\cos\Omega t)x'-(\sin\Omega t)y'\\ y&=& (\sin\Omega t)x'+(\cos\Omega t)y'\\ z&=& z' \end{eqnarray} となります。
\(K\) 系での4元ポテンシャルの反変成分は \[ A^0=0,\quad A^1=0,\quad A^2=0,\quad A^3=By \] ととることができます。ミンコフスキー計量の符号を \(\eta_{00}=-1\)、\(\eta_{11}=1\)、\(\eta_{22}=1\)、\(\eta_{33}=1\) ととることにすると、4元ポテンシャルの共変成分も \[ A_0=0,\quad A_1=0,\quad A_2=0,\quad A_3=By \] となります。
ここで \(K\) 系の座標と \(K'\) 系の座標との関係を見ると、\(ct\)、\(x\)、\(y\) は \(z\) に依存せず、また \(z'\) は \(ct'\)、\(x'\)、\(y'\) に依存しないことがわかります。よって、\(K'\) 系での4元ポテンシャルの共変成分も \[ A'_0=0,\quad A'_1=0,\quad A'_2=0,\quad A'_3=By \] すなわち \[ A'_0=0,\quad A'_1=0,\quad A'_2=0,\quad A'_3=B((\sin\Omega t)x'+(\cos\Omega t)y') \] となります。
電磁場テンソルは、非慣性系であっても \[ F'_{\mu\nu}=\frac{\partial A'_\nu}{\partial x'^\mu}-\frac{\partial A'_\mu}{\partial x'^\nu} \] で与えられるので[1]、 \[ F'_{\mu\nu}=\left( \begin{array}{cccc} 0 & 0 & 0 & \displaystyle\frac{B\Omega}{c}((\cos\Omega t)x'-(\sin\Omega t)y') \\ 0 & 0 & 0 & B\sin\Omega t\\ 0 & 0 & 0 & B\cos\Omega t\\ \displaystyle\frac{B\Omega}{c}(-(\cos\Omega t)x'+(\sin\Omega t)y') & -B\sin\Omega t & -B\cos\Omega t & 0 \end{array} \right) \] となり、\(K'\) 系での電場と磁場は \[ \boldsymbol{E}'=(0,\ 0,\ B\Omega(-(\cos\Omega t)x'+(\sin\Omega t)y')),\quad \boldsymbol{B}'=(B\cos\Omega t,\ -B\sin\Omega t,\ 0) \] となります。
コイル上では \(x'=0\) なので \begin{eqnarray} \int_{\mathrm{P}\rightarrow\mathrm{Q}}\boldsymbol{E}'\cdot d\boldsymbol{r}'&=& 0\\ \int_{\mathrm{Q}\rightarrow\mathrm{R}}\boldsymbol{E}'\cdot d\boldsymbol{r}'&=& -B\Omega\sin\Omega t\left(-\frac{L_a}2\right)\cdot L_b =\frac{BS\Omega}2\sin\Omega t\\ \int_{\mathrm{R}\rightarrow\mathrm{S}}\boldsymbol{E}'\cdot d\boldsymbol{r}'&=& 0\\ \int_{\mathrm{S}\rightarrow\mathrm{P}}\boldsymbol{E}'\cdot d\boldsymbol{r}'&=& B\Omega\sin\Omega t\cdot\frac{L_a}2\cdot L_b =\frac{BS\Omega}2\sin\Omega t \end{eqnarray} よって、コイルに生じる起電力は \[ \oint\boldsymbol{E}'\cdot d\boldsymbol{r}'=BS\Omega\sin\Omega t \] となり、「その1」で得られた結果に一致します。
また、コイルが囲む面上で磁場を積分すると \[ \int\boldsymbol{B}'\cdot d\boldsymbol{S}'=BS\cos\Omega t \] となるので、確かに \[ \oint\boldsymbol{E}'\cdot d\boldsymbol{r}'=-\frac d{dt}\int\boldsymbol{B}'\cdot d\boldsymbol{S}' \] が成り立っています。
脚注
- ^ L. D. ランダウ、E. M. リフシッツ『場の古典論』(東京図書、1978年)、式 (90.1) とその前後を参照してください。